Python Quadratic Formula: A Comprehensive Tutorial

Read Time:5 Minute, 50 Second

In this article, our focus will be on harnessing Python to tackle quadratic equations—a fundamental concept in algebra. Distinguished by its second-degree polynomial nature, quadratic equations are pervasive in mathematical applications, setting them apart from the more straightforward linear counterparts.

Throughout this tutorial, we’ll leverage Python’s built-in math library to navigate the intricacies of solving quadratic equations. Additionally, we’ll employ numpy for efficient array manipulation and utilize matplotlib to visualize the graphical representation of quadratic equations within the Python ecosystem.

For those yet to have these essential libraries installed, we’ll guide you through the process in the subsequent steps. Please proceed to your “Command Prompt” (for Windows users) and use the provided code snippet for installation.

pip install numpy

pip install matplotlib

The Quadratic Equation Formula

Let’s delve into the quadratic formula and start by grasping the standard form of a quadratic equation:

ax^2 + bx + c = 0

Here, a, b, and c represent real numbers, with the condition that ‘a’ must not equal zero.

Now, the pivotal questions arise: How can we determine if this equation possesses a solution? And if a solution exists, what is the count of these solutions?

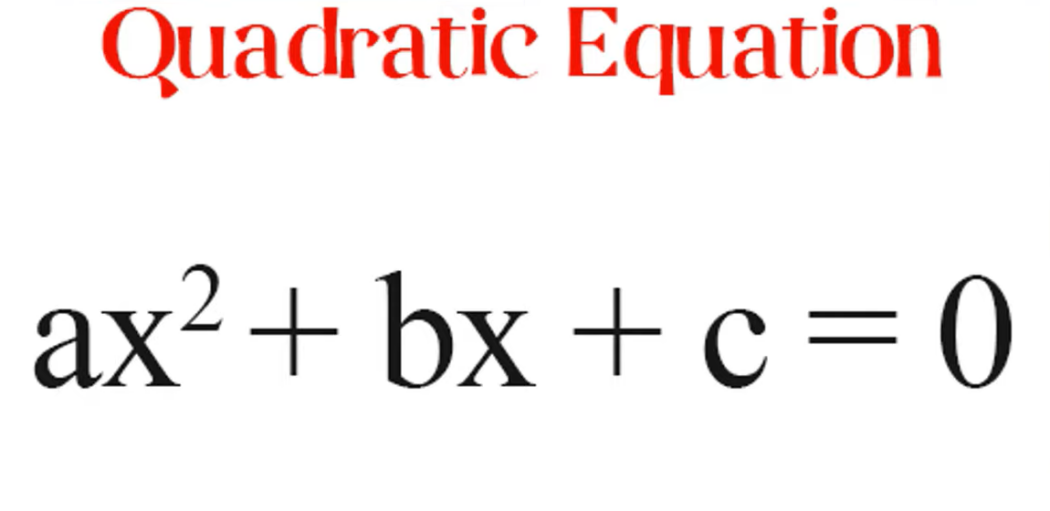
quadratic equation formula ax^2 + bx + c = 0 on plain white background

Solving a Quadratic Equation

Step 1: Computing the Discriminant

The initial phase in solving a quadratic equation involves computing the discriminant. Employing the straightforward formula:

D = b^2 – 4ac

allows us to determine the discriminant’s value. Subsequently, based on this value:

If it’s positive, the equation possesses two solutions;
If it’s zero, the equation exhibits one repeated solution;
If it’s negative, the equation lacks real solutions.

Step 2: Determining x-values

For finding each x-value, we employ the following quadratic formula:

x = (-b ± √(b^2 – 4ac)) / (2a) = (-b ± √D) / (2a)

This translates to:

x1 = (-b + √D) / (2a);
x2 = (-b – √D) / (2a).

These are the essential steps to uncover the solutions for the given quadratic equation.

Solving a Quadratic Equation (Illustration)

To illustrate the process, let’s examine the following quadratic equation:

x^2 – 5x – 14 = 0

In this equation, we have a=1, b=-5, and c=-14.

As our initial step, we will compute the discriminant:

D = b^2 – 4ac = (-5)^2 – 4×1×(-14) = 81

Given that D>0, we can conclude that this equation possesses two distinct roots.

Now, let’s determine the values of x1 and x2:

x1 = (-b + √D) / (2a) = (-(-5) + √81) / (2×1) = 7;
x2 = (-b – √D) / (2a) = (-(-5) – √81) / (2×1) = -2.

Thus, the solution to this equation is: x1=7 and x2=-2

Solving Quadratic Equations with Python

For a practical demonstration, let’s take a look at the following quadratic equation:

x^2 – 5x – 14 = 0

Here, we have the coefficients a=1, b=-5, and c=-14.

Step 1: Prompt the User for Equation Coefficients (a, b, c)

To begin, we must collect these coefficients from the user:

a, b, c = eval(input(“Please enter the a, b, c coefficients of your quadratic equation: “))

In this context, we will provide the three values separated by commas as follows: 1, -5, -14.

It’s essential to emphasize that when values other than real numbers, like strings or booleans, are provided as input, the input function itself won’t trigger an error. However, it’s crucial to recognize that any following mathematical calculations will not produce meaningful results. To address this potential issue, it is strongly recommended to incorporate a comprehensive set of validation checks to ensure the integrity and accuracy of the user’s input data. To mitigate this, it’s advisable to implement a series of checks to validate the user’s input:

check_input = True
while check_input:
    a, b, c = eval(input("Please enter the a, b, c coefficients of your quadratic equation: "))
    try: 
        float(a), float(b), float(c)
        check_input = False
    except ValueError:
        print("Please make sure the coefficients are real numbers and try again")
        check_input = True

Up to this point, a, b, and c variables have been established in Python.

Step 2: Compute the Discriminant with Python

Now, the next task is to compute the discriminant. To achieve this, we’ll employ the math library, which comes prebuilt in Python, and utilize its square root function:

from math import sqrt

disc = b*b-4*a*c

For the previously input values, the discriminant should have a value of 81.

Step 3: Determine Quadratic Equation Roots with Python

Now, we proceed to solve for the roots of the equation. It’s crucial to remember that we must also verify whether the discriminant is less than zero, indicating that the quadratic equation possesses no solutions:

if disc >=0:
    x1 = (-b+sqrt(disc))/(2*a)
    x2 = (-b-sqrt(disc))/(2*a)
    print("The roots of the equation are:", x1, x2)
else:
    print("The equation has no solutions")

In this example, the obtained values are x1=7 and x2=−2.

Creating a Graph of a Quadratic Function with Python

The graphical depiction of a quadratic equation takes the form of a parabola;

When we simplify the quadratic equation to equality with zero, its roots correspond to the points where the curve intersects the y-axis;

To visualize the quadratic equation discussed earlier, we will utilize Python for plotting and pinpointing the root locations.

Our initial step involves importing the necessary libraries:

import matplotlib.pyplot as plt
import numpy as np

Now, we’ll define the range along the `x-axis` that we want to analyze. In this instance, we’ll choose a range spanning from -10 to 15:

x = np.linspace(-10, 15)

Now, we can construct our function for y using the parameters discussed in the preceding section:

y = x**2 - 5*x - 14

Initially, the x-axis and y-axis will be plotted as dashed lines, accompanied by the axis labels.

plt.hlines(y=0, xmin=min(x), xmax=max(x), linestyles='dashed')
plt.vlines(x=0, ymin=min(y), ymax=max(y), linestyles='dashed')
plt.xlabel('x')
plt.ylabel('y')

Subsequently, plot the parabolic curve.

plt.plot(x, y)
plt.show()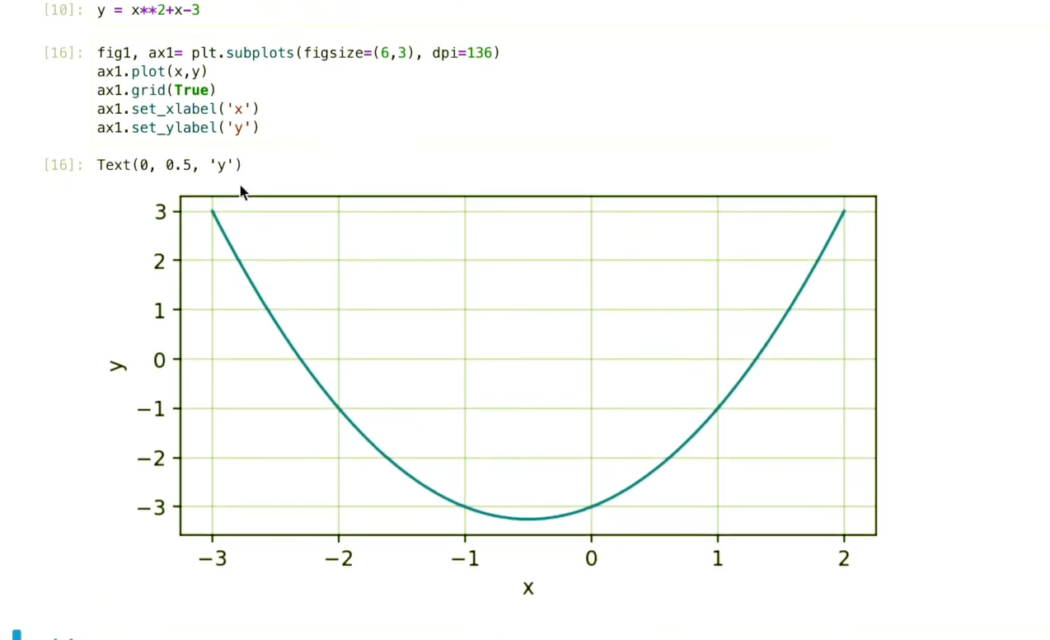

Python Program for Solving Quadratic Equations

from math import sqrt

check_input = True
while check_input:
    a, b, c = eval(input("Please enter the a, b, c coefficients of your quadratic equation: "))
    try: 
        float(a), float(b), float(c)
        check_input = False
    except ValueError:
        print("Please make sure the coefficients are real numbers and try again")
        check_input = True

disc = b*b-4*a*c

if disc >= 0:
    x1 = (-b+sqrt(disc))/(2*a)
    x2 = (-b-sqrt(disc))/(2*a)
    print("The roots of the equation are:", x1, x2)
else:
    print("The equation has no solutions")

Conclusion

In this article, we have explored the process of solving quadratic equations utilizing Python and the math library. This knowledge not only empowers you to tackle quadratic equations but also provides a foundation for solving a wide range of mathematical problems using programming. The versatility of Python, coupled with its mathematical libraries, opens up a world of possibilities for problem-solving and data analysis in various domains.