Vector Multiplication in Python: A Guide

In the realm of data science and mathematics, vector multiplication is a fundamental operation. Python, as a versatile programming language, provides various tools and libraries to work with vectors and perform multiplication operations. In this comprehensive guide, we will delve into the world of vector multiplication in Python, exploring its various aspects and applications.

Understanding Vectors

Before diving into vector multiplication, let’s establish a solid foundation by understanding what vectors are and how they are represented in Python.

What Are Vectors?

In mathematics, vectors are mathematical objects used to represent quantities that have both magnitude and direction. In Python, vectors are typically represented as arrays or lists, where each element corresponds to a component of the vector.

Vector Representation in Python

In Python, you can represent a vector using various data structures, such as lists or NumPy arrays. Let’s explore both methods:

Using Lists

Using NumPy Arrays

Vector Multiplication Techniques

Vector multiplication comes in different flavors, each serving a specific purpose. We’ll explore the most common types of vector multiplication in Python:

1. Scalar Multiplication

Scalar multiplication involves multiplying a vector by a scalar (a single numerical value). This operation scales the vector by the scalar factor.

Example:

2. Dot Product (Scalar Product)

The dot product, also known as the scalar product, calculates the sum of the products of corresponding elements of two vectors.

Example:

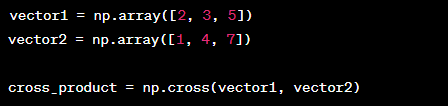
3. Cross Product (Vector Product)

The cross product calculates a new vector that is orthogonal (perpendicular) to the two input vectors. This operation is commonly used in 3D geometry.

Example:

Applications of Vector Multiplication

Vector multiplication plays a vital role in various fields and applications. Let’s explore some practical use cases:

1. Physics and Engineering

In physics and engineering, vector multiplication is used to calculate forces, moments, and angular velocities in mechanical systems.

2. Machine Learning

In machine learning, vector operations are fundamental for data preprocessing, feature engineering, and neural network computations.

3. Computer Graphics

Vector multiplication is essential for rendering 2D and 3D graphics, transforming objects, and simulating lighting effects.

Python Libraries for Vector Operations

Python offers powerful libraries that simplify vector operations. The most commonly used library is NumPy.

NumPy for Vector Operations

NumPy is a robust library that provides efficient tools for performing vector operations. It offers functions like dot, cross, and multiply for working with vectors.

Vector Operations and Properties

Now that we have covered the basics of vector multiplication, it’s important to delve deeper into some key vector operations and properties. Understanding these concepts will enable you to work with vectors more effectively.

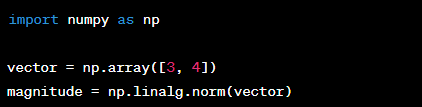
Vector Magnitude

The magnitude of a vector, often denoted as |v|, represents the length or size of the vector. In Python, you can calculate the magnitude of a vector using the Euclidean norm or the L2 norm.

Euclidean Norm (L2 Norm)

The Euclidean norm of a vector v = [x1, x2, …, xn] is calculated as:

 ∣v∣= x1 2 +x2 2 +…+xn 2

Example:

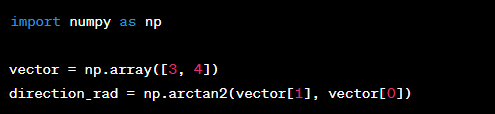
Vector Direction

The direction of a vector is defined by the angle it makes with respect to a reference axis. You can use trigonometric functions like arctan to find the direction of a vector.

Example:

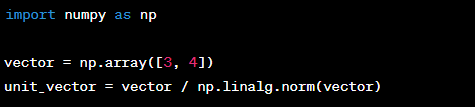
Unit Vectors

A unit vector is a vector with a magnitude of 1 and points in a specific direction. It is often used to represent direction in vector operations.

Example:

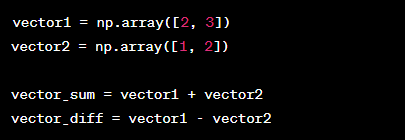
Vector Addition and Subtraction

Vector addition and subtraction are fundamental operations in linear algebra. When adding or subtracting vectors, corresponding elements are combined or subtracted.

Example:

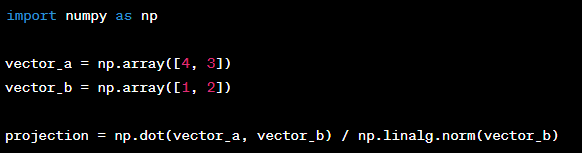
Vector Projection

Vector projection is used to find the component of one vector in the direction of another vector. It’s a valuable tool in physics and engineering.

Example:

Properties of Vector Multiplication

Vector multiplication exhibits several important properties that make it a powerful mathematical tool.

Distributive Property

Vector multiplication, like scalar multiplication, follows the distributive property. This means that vector addition and multiplication can be distributed over each other.

Example:

a ⋅( b + c )= a ⋅ b + a ⋅ c 

Commutative Property

The dot product of two vectors is commutative, meaning the order of multiplication does not matter.

Example:

a⋅b=b⋅a

Scalar Multiplication of the Dot Product

Scalar multiplication can be distributed into the dot product of two vectors.

Example:

c⋅(a⋅b)=(a⋅b)⋅c

Magnitude and Dot Product

The dot product of two vectors is related to their magnitudes and the angle between them through the cosine of the angle.

Example:

a⋅b=∣a∣⋅∣b∣⋅cos(θ)

Applications in Data Science

Vector multiplication is a fundamental concept in data science and machine learning. It plays a crucial role in various applications, including:

• Feature Engineering: Transforming and combining features using vector operations to improve model performance;
• Matrix Operations: Performing matrix-vector multiplications for linear transformations and solving linear equations;
• Dimensionality Reduction: Utilizing vector operations for techniques like Principal Component Analysis (PCA).

Python Libraries for Linear Algebra

In addition to NumPy, there are other Python libraries that specialize in linear algebra and vector operations:

1. SciPy

SciPy builds on NumPy and provides additional functionality for scientific and technical computing, including optimization, integration, and signal processing.

2. SymPy

SymPy is a symbolic mathematics library that allows you to perform symbolic algebra, making it suitable for symbolic vector manipulation.

3. TensorFlow and PyTorch

These deep learning frameworks include powerful tools for automatic differentiation and tensor operations, making them ideal for advanced machine learning applications.

Advanced Vector Multiplication Techniques

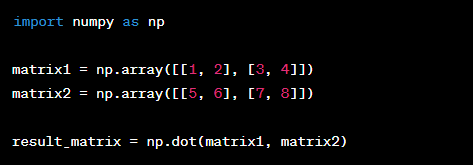
Matrix Multiplication

Matrix multiplication is a critical operation in linear algebra, and it involves multiplying two matrices to produce a new matrix. In Python, you can perform matrix multiplication using libraries like NumPy.

Matrix multiplication is particularly important in data science for tasks such as linear regression, image processing, and network analysis. It allows you to transform data, apply filters, and perform various transformations efficiently.

Example:

Vectorization for Speed

Vectorization is a technique that leverages the hardware capabilities of modern processors to perform mathematical operations on entire arrays or vectors simultaneously. This results in significantly faster computations compared to traditional loop-based operations.

In Python, libraries like NumPy are optimized for vectorized operations, making it possible to work with large datasets efficiently.

Broadcasting in NumPy

NumPy allows for broadcasting, a feature that enables the element-wise operations between arrays of different shapes. When performing operations between arrays with different shapes, NumPy automatically expands the smaller array to match the shape of the larger one, making computations more convenient.

Parallelization with NumPy

For computationally intensive tasks involving large datasets, parallelization can be crucial. NumPy can take advantage of multiple CPU cores through parallel computing libraries like Dask and Numexpr, speeding up calculations.

Real-World Applications

Geographic Information Systems (GIS)

In Geographic Information Systems (GIS), vector multiplication is used extensively to analyze geographic data. Operations like spatial joins, buffer calculations, and map projections rely on vector operations to process and manipulate geographical features efficiently.

Financial Modeling

Financial analysts and quants use vector multiplication in Python to model complex financial systems. It helps in portfolio optimization, risk assessment, and options pricing by performing matrix calculations on historical data.

Game Development

In the world of game development, vector operations are essential for physics simulations, collision detection, and character animations. Game engines like Unity and Unreal Engine often utilize vector mathematics to create realistic gaming experiences.

Image Processing

In image processing, vector multiplication is used for tasks like image transformation, edge detection, and image enhancement. Libraries like OpenCV and Pillow provide tools to perform vector operations on images efficiently.

Performance Optimization and Efficiency

NumPy Optimizations

NumPy, being a highly optimized library, offers various techniques to improve the performance of vector operations. It leverages low-level, highly optimized C and Fortran libraries, making it incredibly efficient. However, you can further enhance performance by considering the following:

NumPy Universal Functions (ufuncs)

NumPy ufuncs are precompiled functions that operate on NumPy arrays element-wise. They are significantly faster than equivalent operations performed in Python loops. Utilizing ufuncs for vector operations can greatly boost performance.

Memory Management

Efficient memory management is crucial for performance. Be mindful of unnecessary array copies, and use in-place operations when possible to minimize memory overhead.

Cython for Speed

Cython is a superset of Python that allows you to write C extensions for Python code. It’s an excellent choice for optimizing critical sections of code that involve vector multiplication. By compiling Python code with Cython, you can achieve near-C performance.

Just-In-Time Compilation (JIT)

Tools like Numba and PyPy provide Just-In-Time compilation capabilities. Numba, in particular, is designed to accelerate Python functions, including those involving vector operations. It can be especially beneficial for numerical computations.

Handling Sparse Vectors

Sparse vectors are vectors in which most of the elements are zero. They are common in various domains, including natural language processing and recommendation systems. Handling sparse vectors efficiently can lead to significant memory and computational savings.

Compressed Sparse Formats

To represent sparse vectors, consider using compressed sparse formats like Compressed Sparse Row (CSR) or Compressed Sparse Column (CSC). These formats store only the non-zero elements and their positions, reducing memory usage and speeding up operations.

Sparse Matrix Multiplication

When working with sparse vectors, you may encounter scenarios where you need to multiply them with dense matrices efficiently. Libraries like SciPy provide optimized functions for sparse matrix-vector multiplication (SpMV), which is a fundamental operation in many applications.

Error Handling and Debugging

Debugging Vector Operations

Debugging vector operations can be challenging due to the complexity of numerical computations. However, there are strategies to simplify the process:

Check Data Types

Ensure that the data types of vectors and matrices are compatible for the intended operations. Mismatches can lead to unexpected errors.

Inspect Intermediate Results

When encountering errors, inspect intermediate results to identify where the issue occurs. Print or visualize intermediate variables to gain insights into the problem.

Handling Numerical Instabilities

Vector operations involving floating-point numbers can sometimes lead to numerical instabilities. These issues can manifest as NaNs (Not-a-Number) or infinite values. To address these problems, consider:

Numerical Precision

Adjust the numerical precision by changing the data type or using libraries like NumPy’s np.finfo to control the tolerance for comparisons.

Regularization

In some applications, regularization techniques can be applied to stabilize numerical calculations, especially in machine learning and optimization problems.

Conclusion

Vector multiplication in Python is a versatile and crucial operation used in various fields, from mathematics to computer graphics and machine learning. Understanding the different types of vector multiplication and their applications is essential for any Python developer or data scientist.

Now that you’ve gained a comprehensive understanding of vector multiplication in Python, you’re ready to apply these concepts to your own projects. Happy coding!

Happy

0 0 %

Sad

0 0 %

Excited

0 0 %

Sleepy

0 0 %

Angry

0 0 %

Surprise

0 0 %