
Calculate Hadamard Product using Python
In the vast realm of mathematical operations, the Hadamard product holds a special place. It’s a fundamental concept in linear algebra and is often used in various scientific fields, including quantum computing and signal processing. In this comprehensive guide, we will explore how to calculate the Hadamard product using Python. Whether you’re a seasoned coder or a newcomer, this step-by-step tutorial will empower you with the skills to harness the potential of Python for this mathematical operation.
What is the Hadamard Product?
The Hadamard product, also known as the element-wise product or Schur product, is a binary operation that takes two matrices of the same dimensions and produces a third matrix, where each element is the product of the corresponding elements of the input matrices. It’s denoted by ⊙ or sometimes by * (asterisk).
For instance, given two matrices A and B:
Matrix A:
| 2 | 4 |
| 6 | 8 |
Matrix B:
| 1 | 3 |
| 5 | 7 |
The Hadamard product of A and B would be:
Matrix C:
| 2*1 | 4*3 |
| 6*5 | 8*7 |
Now, let’s dive into the Python code to perform this operation.
Setting Up Your Python Environment
Before we start calculating the Hadamard product, make sure you have Python installed on your system. You can download it from the official Python website.
Writing Python Code for Hadamard Product
To calculate the Hadamard product in Python, you can use the NumPy library, which provides powerful tools for working with arrays and matrices. If you don’t have NumPy installed, you can install it using pip:

Now, let’s write the Python code to calculate the Hadamard product of two matrices.
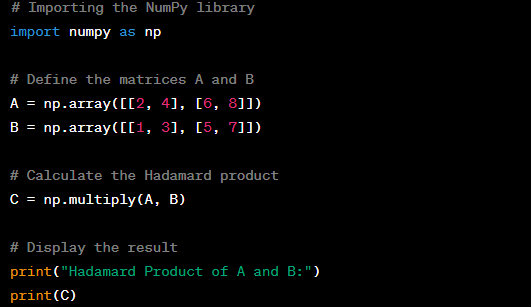
In this code, we first import the NumPy library and define our matrices A and B as NumPy arrays. Then, we use the np.multiply function to calculate the Hadamard product and display the result.
Understanding the Output
When you run the code, you’ll get the Hadamard product matrix C:

Applying Hadamard Product in Machine Learning
The Hadamard product isn’t just a mathematical curiosity; it plays a crucial role in machine learning and data science. Here’s how it can be applied:
Feature Engineering
- Element-wise Feature Scaling: In some cases, you might want to scale features differently. The Hadamard product allows you to apply unique scaling factors to each feature, providing fine-grained control;
- Creating Interaction Features: By taking the Hadamard product of two feature vectors, you can capture their interaction. This can be beneficial when you suspect that the interaction between certain features is essential for your model’s performance.
Regularization Techniques
- L1 Regularization (Lasso): Lasso regularization includes the absolute values of coefficients in the cost function. You can use the Hadamard product to introduce L1 regularization, making some coefficients exactly zero, effectively performing feature selection;
- L2 Regularization (Ridge): Similar to L1, you can incorporate L2 regularization using the Hadamard product to control the magnitude of coefficients.
Data Preprocessing
- Data Cleaning: When dealing with missing values, the Hadamard product can be used to fill in missing data points based on similar records;
- Dimensionality Reduction: Applying the Hadamard product to a matrix with itself (e.g., X ⊙ X) can be used in Principal Component Analysis (PCA) to find the eigenvalues and eigenvectors efficiently.
Recommendation Systems
- User-Item Interaction: In collaborative filtering-based recommendation systems, the Hadamard product is often used to measure the similarity between users and items, providing personalized recommendations;
- Content-Based Filtering: When recommending items based on their attributes, the Hadamard product can be used to calculate the similarity between item features and user preferences.
Conclusion
Congratulations! You’ve learned how to calculate the Hadamard product using Python. This fundamental mathematical operation has applications in various fields, including linear algebra, quantum computing, and image processing. Python’s NumPy library makes it easy to perform this operation efficiently.
Now, you can incorporate the Hadamard product into your data analysis or scientific computing projects. If you found this guide helpful, don’t forget to hit the like button to show your support!
Frequently Asked Questions
The Hadamard product is used for element-wise multiplication of matrices and has applications in linear algebra, quantum computing, signal processing, and image processing.
While NumPy simplifies the process, you can implement the Hadamard product in Python without it, but it may require more manual coding.
Yes, it’s also known as the element-wise product or Schur product.
The Hadamard product is used in image processing for tasks like image enhancement and filtering. It’s also used in quantum computing for quantum gates and operations.
To delve deeper into matrix operations in Python, consider exploring topics like matrix multiplication, eigenvalues, and eigenvectors, as well as other linear algebra concepts.


Average Rating