Levene Test Interpretation: Variance Equality in Python

Read Time:8 Minute, 0 Second

In the field of statistics, there is a critical assumption that underlies the integrity of numerous statistical analyses, including but not limited to analysis of variance (ANOVA) and t-tests. This assumption assumes that the variances in the various groups or populations under study are approximately equal.

The importance of this assumption is that it can ensure the validity and reliability of statistical conclusions. However, if this assumption is violated, it can lead to erroneous conclusions and deprive the results of reliability. To test for equality of variance between several groups or populations, statisticians usually use Levene’s test, a rigorous statistical test designed for this very purpose.

Why is Variance Equality Important?

Before delving into the intricacies of Levene’s test, it is important to understand the key role that the assumption of equality of variance plays in statistics. This assumption is of paramount importance when testing hypotheses and constructing confidence intervals. These statistical procedures are based on the assumption that different populations or groups under study have approximately equal variance. The significance of this assumption is that it ensures that each group contributes fairly and unbiasedly to the overall statistical analysis.

However, when the presumption of equal variances is violated, it entails a whole range of potential problems, manifested primarily in two different but interrelated issues:

Type I error: The first problem occurs when a statistical test falsely identifies a significant difference between groups or populations by attributing it to unequal variance, even when no real difference exists. This is essentially a false positive result, falsely claiming the existence of an effect;

Type 2 error: In contrast, a second difficulty arises when a test fails to detect a valid difference between groups or populations, even though such a difference is clearly present. Unequal variance exacerbates this problem, reducing the power of the statistical test and making it less effective at detecting valid effects. In this case, we are talking about a false negative result that does not account for the real effect.

To circumvent these pitfalls and maintain the integrity of the statistical analysis, the equality of variances must be carefully checked and confirmed. The Levene’s test is a powerful tool designed for this very purpose, allowing us to assess whether the variance between several groups or populations meets the required assumption of equality.

Understanding Levene’s Test

The Levene’s test, developed by Howard Levene in 1960, is a hypothesis test to determine whether the variances of several groups or populations are statistically different. The null hypothesis (0H0) in Levene’s test states that the variances of all groups are equal, while the alternative hypothesis (1H1) states that at least one of the groups has a different variance.

The Levene’s Test Statistic

The test statistic in Levene’s test has an F-distribution. To perform the test, it is necessary to calculate the test statistic and compare it with the critical value from the F-distribution based on the chosen significance level (usually 0.05). If the calculated test statistic exceeds the critical value, the null hypothesis is rejected, indicating that there is an inequality of variance.

The Levene’s test statistic is calculated by comparing the absolute deviations of individual data points from their group mean to the overall mean (also called the grand mean). The test statistic is defined as:

W=(k−1)(N−k)∑i=1k∑j=1ni(∣Yij−Yˉi⋅∣)∑i=1k∑j=1ni(∣Yij−Yˉi⋅∣−∣Yi⋅−Yˉ⋅⋅∣)

W – test statistic.

N – total number of observations.

k – number of groups or populations.

n is the number of observations in the i-th group.

Yij represents the 1st observation in the i-th group.

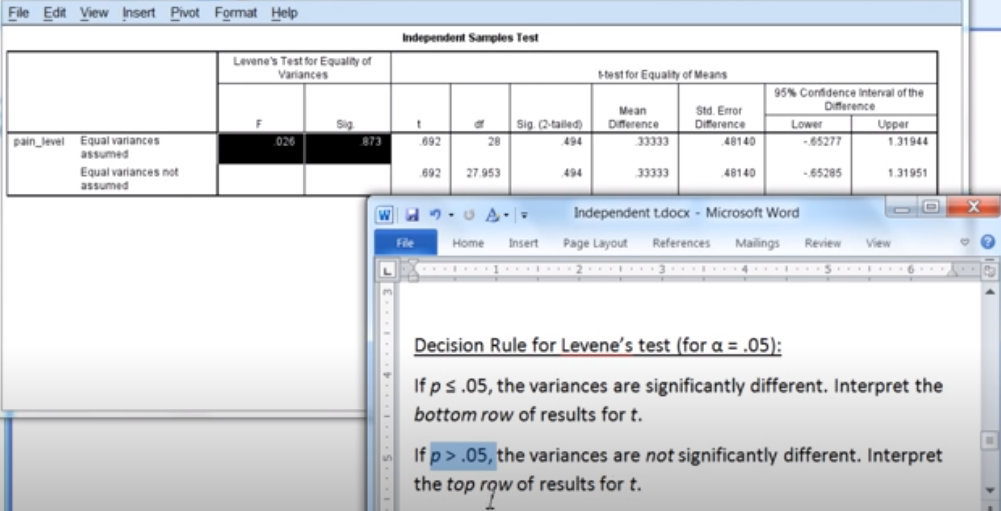
Interpretation

The Levene’s test statistic is calculated by comparing the absolute deviations of individual data points from their group mean to the overall mean (also called the grand mean).

To interpret the results of the Levene’s test, it is necessary to compare the calculated test statistic

W with the critical value from the F-distribution at a given level of significance (α). If W is greater than the critical value, the null hypothesis is rejected (0H0) and it is concluded that at least one of the groups has different variance.

Performing Levene’s Test in Python

Now let’s see how to perform Levene’s test in Python using the popular statistics library scipy. We will go through the example step by step.

Step 1: Import Libraries

First, we need to import the necessary libraries. In this case we import scipy to run the test and numpy to create sample data.

import numpy as np
from scipy.stats import levene

Step 2: Generate Sample Data

To demonstrate, let’s create some sample data. Let’s simulate three groups with different dispersions.

# Seed for reproducibility
np.random.seed(42)

# Generate three groups of data with different variances
group1 = np.random.normal(0, 1, 100)  # Mean=0, Variance=1
group2 = np.random.normal(0, 2, 100)  # Mean=0, Variance=4
group3 = np.random.normal(0, 0.5, 100)  # Mean=0, Variance=0.25

Step 3: Perform Levene’s Test

Now that we have sample data, we can perform Levene’s test to assess equality of variance.

# Perform Levene's Test
statistic, p_value = levene(group1, group2, group3)

Step 4: Interpret the Results

Finally, we can interpret the results based on the p-value obtained from the test.

alpha = 0.05  # Significance level

if p_value < alpha:
    print("Reject the null hypothesis: Variances are not equal.")
else:
    print("Fail to reject the null hypothesis: Variances are equal.")

In this example, if the p-value is less than the significance level (α), we reject the null hypothesis, indicating that at least one group has different variance. Otherwise, if the p-value is greater than or equal to α, we do not reject the null hypothesis, suggesting that the variances are equal.

Example: Levene’s Test in Real Data Analysis

Let’s apply Levene’s test to a real data set to evaluate equality of variance. We will use the Iris dataset, popular in machine learning and statistics, containing measurements of sepal and petal lengths and widths for three species of iris flowers.

Step 1: Import Libraries

import numpy as np
from scipy.stats import levene

Step 2: Load the Iris Dataset

# Seed for reproducibility
np.random.seed(42)

# Generate three groups of data with different variances
group1 = np.random.normal(0, 1, 100)  # Mean=0, Variance=1
group2 = np.random.normal(0, 2, 100)  # Mean=0, Variance=4
group3 = np.random.normal(0, 0.5, 100)  # Mean=0, Variance=0.25

Step 3: Perform Levene’s Test

We perform Levene’s test to assess the equality of variance for sepal length of three iris species.

# Perform Levene's Test
statistic, p_value = levene(group1, group2, group3)

Step 4: Interpret the Results

alpha = 0.05  # Significance level

if p_value < alpha:
    print("Reject the null hypothesis: Variances are not equal.")
else:
    print("Fail to reject the null hypothesis: Variances are equal.")

In this example, if the p-value is less than 0.05, we can conclude that the variation in sepal length for the three iris species is not equal. If the p-value is greater than or equal to 0.05, we can conclude that the variations are equal.

What does it mean if the Levene’s test is significant?

If the results of Levene’s test are significant, it means that there are grounds to reject the null hypothesis. In the context of Levene’s equality of variance test, a significant result means that at least one of the groups or populations being compared has a significantly different variance from the others. In other words, the variance is not equal in all groups.

The following is a description of what a significant result means in Levene’s test:

Rejection of the null hypothesis: The null hypothesis (0H0) in Levene’s test states that all groups have equal variance. If the test is significant, you have enough evidence to conclude that the assumption of equal variance is not met.

Unequal variances: The significance of Levene’s test indicates that there are statistically significant differences in the variance of at least one pair of groups. It does not indicate which groups have different variances, only that there is a difference somewhere.

Caution in subsequent analyses: If the Levene’s test turns out to be significant, this result should be taken into account in further statistical analysis. If further analyses involving equal variance (e.g., ANOVA or t-tests) are continued, the results may be unreliable or biased. In such cases, it may be necessary to seek alternative statistical methods that do not assume equal variances.

Overall, Levene’s significant test indicates that caution should be exercised when using statistical tests that assume equal variance, as this assumption is likely to be violated. It may be necessary to adapt the analysis approach or select alternative statistical tests that are more robust to unequal variance.

Conclusion

The Levene’s test for equality of variance is a valuable statistical tool for assessing whether the variances of several groups or populations are statistically different. Ensuring equality of variance is critical to the validity of various statistical tests, including ANOVA and t-tests.

In this paper, we reviewed the importance of equality of variance and provided a detailed introduction to the Levene’s test, including its statistics and interpretation. In addition, we demonstrated how to perform Levene’s test in Python using the scipy library, both on synthetic data and on a real dataset.

Incorporating Levene’s test into the data analysis process will allow for more informed decisions about the choice of statistical tests and ensure the reliability of statistical inference.