Transpose Matrix using Python: A Comprehensive Guide

Read Time:4 Minute, 49 Second

Understanding how to transpose a matrix is a foundational skill in linear algebra, and its application in Python is equally significant. This ultimate guide aims to demystify the techniques for reorienting matrices in Python, covering methods from simple one-liners to more complex algorithms.

Whether you’re a student delving into linear algebra or a professional seeking to optimize data processing, this guide offers something of value for you.

Understanding Matrix Transposition

Matrix transposition is the process of switching the rows and columns of a given matrix. This action is particularly important in the realms of computer science, data science, and linear algebra. Here are key points that help one grasp the essence of matrix transposition:

Row-to-Column Transformation: In a transposed matrix, the rows of the original matrix become columns;
Square and Non-Square Matrices: Transposition works on both square (equal number of rows and columns) and non-square matrices;
Main Diagonal: The transposition process rotates the elements of a matrix across the main diagonal.

https://youtube.com/watch?v=mAz1129fjTA%3Fsi%3DkXcaXeDFrB77B-S3

Implementing Matrix Transposition in Python

Python offers multiple ways to achieve matrix reorientation. Here are some methods to perform this operation:

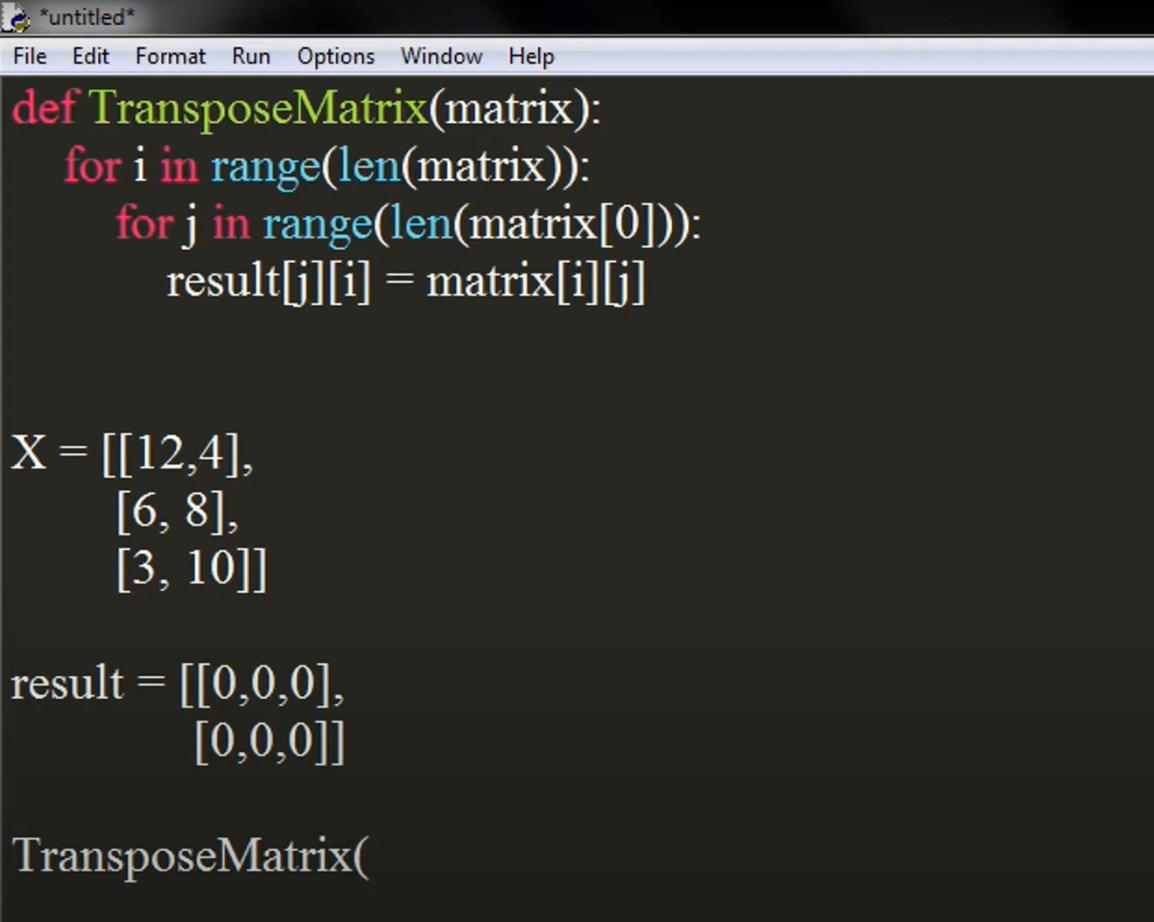
Using Nested List Comprehensions: One of the simplest techniques for small-sized matrices.

transposed = [[row[i] for row in original_matrix] for i in range(len(original_matrix[0]))]

Utilizing NumPy Library: For larger matrices, leveraging the NumPy library is often more efficient.

import numpy as np
transposed = np.transpose(original_matrix)

Applying zip Function: Python’s built-in zip function can also be employed for this purpose, especially when working with lists.

transposed = list(map(list, zip(*original_matrix)))

Optimization Strategies

Efficiency is key when dealing with large-scale data transformation tasks. Here are some tips for maximizing performance:

Avoid Loops for Large Matrices: Iterating through each element can be time-consuming; consider leveraging libraries like NumPy for optimized operations;
Memory Management: Be cautious about memory utilization, especially when transposing very large matrices;
Parallel Processing: Consider parallelizing the computation for significantly large matrices to reduce the time complexity.

Algorithmic Approaches for Matrix Reorientation

Matrix transposition doesn’t always have to rely on conventional methods. Advanced algorithms offer opportunities for optimization, especially when dealing with matrices of larger dimensions. Let’s explore some of these methods in greater detail:

Strassen’s Algorithm

This algorithm primarily focuses on matrix multiplication but can be adapted for transposition. Strassen’s algorithm reduces the number of recursive multiplication calls, making it faster than the conventional methods for large matrices.

Block Matrix Transposition

In this approach, the matrix is divided into smaller “blocks” or sub-matrices, and transposition occurs within each block. This method is particularly effective for large matrices stored in external memory, where loading the entire matrix into RAM isn’t feasible. Block transposition minimizes the I/O operations, thereby increasing efficiency.

In-Place Matrix Reorientation

Conventional methods often require additional memory space for storing the transposed matrix. However, in-place algorithms enable the reorientation of the matrix using zero or minimal extra memory, which is advantageous for systems with memory constraints.

Each of these advanced algorithms serves a specific need and can be more efficient than traditional methods under certain conditions.

Applications of Matrix Transposition

The practice of matrix reorientation transcends academic interest; it has practical implications across various fields.

Data Science

In data science, matrix transposition is often used for data normalization, where feature scaling is crucial. Transposing a matrix also aids in restructuring data, which is invaluable for tasks such as recommendation systems or social network analysis.

Machine Learning

In machine learning, particularly in unsupervised learning algorithms like Principal Component Analysis (PCA), matrix reorientation plays a vital role. Transposing the covariance matrix is an essential step in calculating the eigenvalues and eigenvectors, which are fundamental to the dimensionality reduction process.

Signal Processing

Matrix transposition is commonly used in image and digital signal transformations. In image processing, for example, transposing matrices can help in rotating the image around its central axis, which is essential in tasks like object recognition or tracking.

Comparing Matrix Transposition Libraries

There’s no one-size-fits-all when it comes to choosing a Python library for matrix transposition. Different libraries offer different advantages:

NumPy

Renowned for its speed and efficiency, NumPy is the go-to library for numerical computations in Python. It provides a highly optimized transpose function, suitable for both small and large matrices. NumPy operations are implemented in C, providing a speed advantage.

TensorFlow

TensorFlow, primarily known for deep learning applications, also offers matrix transposition functions. While it’s not as lightweight as NumPy, it provides the benefit of hardware acceleration through GPUs, making it useful for very large matrices.

PyTorch

Similar to TensorFlow but more Pythonic in its approach, PyTorch is another excellent option. It also offers GPU support and is particularly useful if you’re already using PyTorch for machine learning tasks, providing a unified environment.

Choosing the right library depends on your specific requirements, whether it’s speed, ease of use, or the ability to handle large-scale data efficiently. Therefore, understanding the strengths and limitations of each can guide you to make an informed decision.

Conclusion

Transposing matrices in Python can be performed through a variety of methods, from elementary to advanced, depending on the requirements and the nature of the data in question. Whether one opts for list comprehensions for small matrices or specialized algorithms for data-heavy tasks, it’s crucial to keep performance considerations like speed and memory in mind.

This guide aims to serve as a complete resource for both newcomers and experts, covering not just the ‘how’ but also the ‘why’ and ‘when’ of matrix reorientation. With continuous developments in data transformation techniques, staying updated on the latest methods is imperative for any data manipulation task.